About CryptoMathCREST

This research project is supported by CREST - a funding program, which is run by the Japan Science and Technology Agency (JST). The aims of JST are to promote and encourage the development of breakthrough technologies that contribute to attainment of the country’s strategic objectives, and to return the results of such research to the society through innovations.
CREST supports team-oriented research with the aim of achieving the strategic goals set forth by the government. The objective is to create revolutionary technological seeds for science and technology innovation. Detailed information can be found on the JST and CREST websites。

Historically, cryptography provides a good example for applications of number theory - before being applied to cryptography, this theory was believed to have no industrial applications. Currently, the newly developed technologies such as quantum computation or power analysis bring up new security risks for the modern cryptosystems. For addressing these risks, high-performance next-generation cryptosystems must be studied that will require to further develop the mathematical background of modern cryptography. More specifically, in order to avoid the security risks posed by the adversaries with advanced attacking capabilities, we must upgrade our cryptosystems, which will in turn require us to rely on a wide range of mathematical theories.

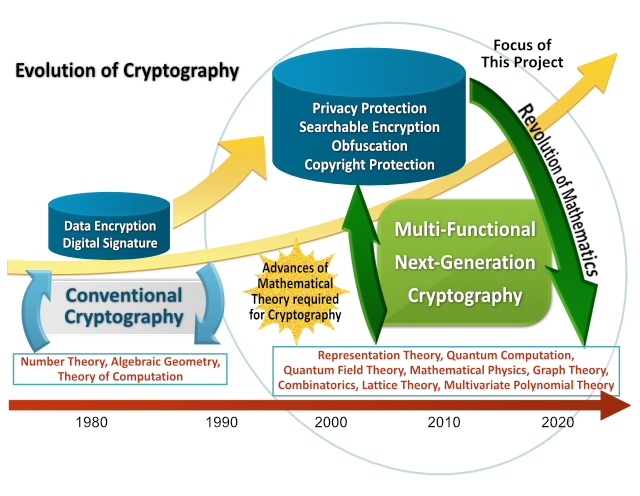
In the recent years, cryptography became concerned with questions beyond secure information transmission, such as privacy-preserving computations and search over encrypted data.
In the 1980-ies and 1990-ies, the major research topics concerned encryption and digital signatures. Then, in the 1990-ies and 2000-s, the interest has shifted towards elliptic curve cryptography, bilinear pairing based cryptography, ID-based encryption, and copyright protection technologies. Then recently, cryptographic techniques found their applications in privacy-preserving technologies, search over private data, obfuscation and others.
In order to address the challenges posed by these new applications, one must rely on a wide range of mathematical theories including representation theory, lattice theory, mathematical physics and others, both for construction of the cryptographic schemes and for their security evaluation. Therefore, one must drastically diversify the range of mathematical theories on which the modern cryptography relies.

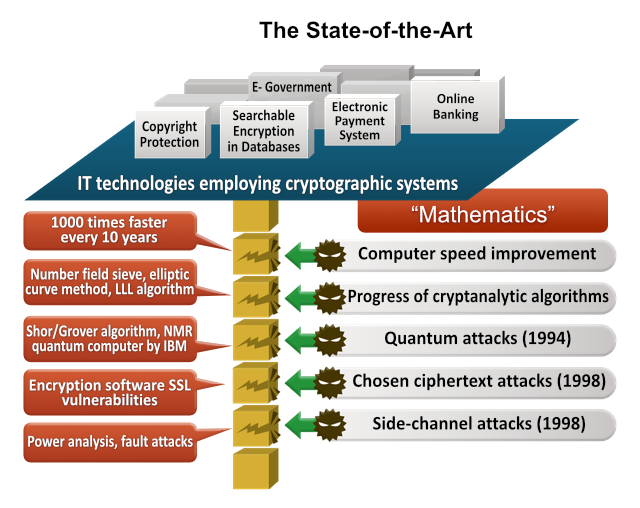
The techniques for cryptanalysis have been developing year-by-year based on the advances in mathematics, hereby permanently posing compromise risks for the employed cryptographic systems. Since 1980-ies, the algorithms such as number field sieve, elliptic curve method, Grobner bases, LLL lattice reduction algorithm and others have been developed and improved, and this process continues presently. In 1994, Shor has introduced a breakthrough algorithm which can solve the factorization and the discrete logarithm problems using the quantum computer.
This showed that in an era with large-scale quantum computers, the security of currently used cryptosystems (such as RSA, elliptic curve cryptography, pairing-based cryptography and some others) will be compromised. In order to avoid these security risks, an adequate security model must be introduced, that would encompass advances in both the cryptanalytic algorithms and the computation technologies.

1. The computer processing performance is growing year by year, hereby steadily increasing the cryptanalytic capability of the attacker. According to the data from the top 500 supercomputer sites (http://www.top500.org), the processing speed is increasing about 1000 times every 10 years.
2. In the 1980-ies, the attention was drawn to the mathematical problems of integer factoring and computing discrete logarithms, since the security of public-key encryption schemes could be based on them. Since then, the efficient attacks algorithms such as number field sieve, elliptic curve method, and LLL lattice reductions algorithms were discovered and improved, giving rise to a new mathematical field of computational number theory.
3. In 1994, Shor proposed a polynomial-time algorithm for solving integer factorization problem on the quantum computer. In 2001, the NMR quantum computer prototype build by IBM was successfully used to implement Shor’s algorithm as a proof of concept.
4. Bleichenbacher presented the chosen ciphertext attack (CCA) and successfully applied to cryptanalyze the SSL software implementation in 1998. Since then, the so called IND-CCA security became a de-facto standard for the public-key encryption.
5. In 1996, the physical attacks on the cryptographic hardware, called the side-channel attacks, were introduced - these included the power analysis and the fault injection attacks. The so called “cold boot” attacks proved particularly effective in deriving partial information about the secret keys of RSA.